MRI K-Space Physics and Applications
K-space is essentially a matrix that stores raw data obtained from the MR scanner. These data are collected during the scanning process, with each point in k-space representing different frequencies and phases of the MR signal emitted by the body being scanned. The data stored in k-space is not in the form of an image but rather in a format that contains all the spatial frequency information needed to reconstruct the image. Understanding and utilizing k-space is fundamental for optimizing MRI techniques and improving image quality
The Physics Behind K-space
The relationship between the data in k-space and the final MR image is mediated through the Fourier transform. The Fourier transform is a mathematical process that converts the spatial frequency data (from k-space) into spatial domain images (the actual MR images seen by radiologists). Each coordinate in k-space corresponds to a sinusoidal wave with a specific frequency and phase, which encodes spatial information about the object being imaged.
Filling K-space: During an MRI scan, gradients modify the magnetic field in a controlled manner along different axes (x, y, and possibly z), which changes the frequencies and phases of the MR signals emitted by the protons in the body. These variations allow different parts of k-space to be filled with corresponding data.
Importance of K-space Distribution: The center of k-space contains lower spatial frequency data, which gives the overall contrast of the image, whereas the outer edges of k-space hold higher spatial frequency data that details edges and fine structures. Thus, how k-space is filled affects the image quality and characteristics such as resolution and contrast.
Practical Applications and Manipulations
In practical MR imaging, the way k-space is sampled and manipulated can significantly affect the final image. Techniques such as adjusting the field of view (FOV), applying different types of filtering (low-pass, high-pass), and using acceleration strategies like partial Fourier imaging directly influence how k-space is filled and therefore the quality and type of images produced. These manipulations can alter spatial resolution, contrast, and the presence of artifacts in the final image.
For example, applying a low-pass filter to k-space data retains low spatial frequencies, enhancing image contrast but potentially losing detail, while a high-pass filter retains high spatial frequencies, enhancing edge details but possibly at the cost of overall image smoothness.
Understanding and utilizing k-space is fundamental for optimizing MRI techniques, improving image quality
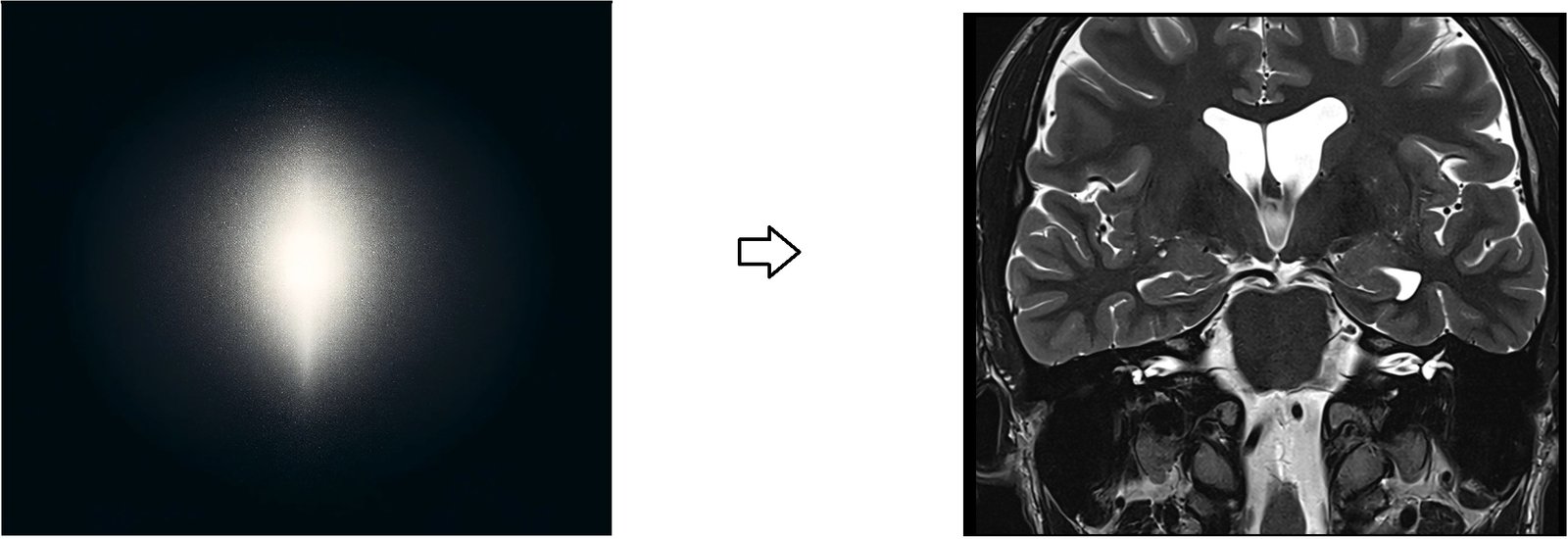
Note ****
The image provided is not an exact representation of k-space; it’s a close graphical approximation of k-space
References
- Moratal, D., Vallés-Luch, A., Martí-Bonmatí, L., & Brummer, M. E. (2008). k-Space tutorial: An MRI educational tool for a better understanding of k-space. Biomedical Imaging and Intervention Journal, 4(1), e15. https://doi.org/10.2349/biij.4.1.e15
- Jornada, T. S., Murata, C. H., & Medeiros, R. B. (2016). Influence of partial k-space filling on the quality of magnetic resonance images. Radiologia Brasileira, 49(3), 158-164. doi: 10.1590/0100-3984.2015.0028. PMCID: PMC4938445, PMID: 27403015.


